分布

离散型

1. (0-1) 分布 (两点分布 / 伯努利分布)

核心逻辑： “只做一次实验”。

试验只有两个结果：成功（记为1）或失败（记为0）。

• 符号： $X\sim B(1,p)$
• 概率分布律：
  • $P(X=1)=p$ （成功的概率）
  • $P(X=0)=1-p$ （失败的概率）
• 数字特征：
  • 期望： $E(X)=p$
  • 方差： $D(X)=p(1-p)$

---

2. 二项分布 (Binomial Distribution)

核心逻辑： “重复做 $n$ 次 (0-1) 实验”。

在 $n$ 次独立重复的伯努利试验中，成功的次数 $X$ 服从二项分布。

• 符号： $X\sim B(n,p)$

• 概率分布律：

  $P(X=k)=C_n^k{p}^k(1-p{)}^{n-k},k=0,1,2,\dots ,n$

  (其中 $C_n^k$ 表示从 $n$ 次中选出 $k$ 次成功)

• 数字特征：

  • 期望： $E(X)=np$
  • 方差： $D(X)=np(1-p)$

• 特例： 当 $n=1$ 时，二项分布就是 (0-1) 分布。

• 两个独立的二项分布随机变量,当它们的第二个参数相同时,其和也服从二项分布

---

3. 泊松分布 (Poisson Distribution)

核心逻辑： “$n$ 很大，但 $p$ 很小的极限情况”（稀有事件）。

通常用于描述单位时间或单位空间内，某事件发生的次数（如：一小时内的电话呼入量、一页书上的错别字数）。

• 符号： $X\sim P(\lambda )$ 或 $X\sim \pi (\lambda )$

• 概率分布律：

  $P(X=k)=\frac{{\lambda }^k}{k!}{e}^{-\lambda },k=0,1,2,\dots$

  (其中 $\lambda$ 是强度参数，代表平均发生的次数)

• 数字特征：

  • 期望： $E(X)=\lambda$
  • 方差： $D(X)=\lambda$ （特征：期望等于方差）

• 若 X 和 Y 相互独立,它们分别服从参数为 λ 1 , λ 2的泊松分布, Z=X+Y服从参数为 λ 1 + λ 2 的泊松分布.

---

一图速览表

分布名称	记号	含义	期望 E(X)	方差 D(X)
0-1 分布	$B(1,p)$	一次成败	$p$	$p(1-p)$
二项分布	$B(n,p)$	$n$ 次成败	$np$	$np(1-p)$
泊松分布	$P(\lambda )$	单位时间内次数	$\lambda$	$\lambda$

连续型

1. 均匀分布 (Uniform Distribution)

核心逻辑： “众生平等”。

• 符号： $X\sim U(a,b)$

• 概率密度函数 (PDF)：

  $f(x)=\{\begin{array}{ll}\frac{1}{b-a},& a<x<b\\ 0,& \text{其他}\end{array}$

• 分布函数 (CDF)：

  在区间 $(a,b)$ 上是线性的，即 $F(x)=\frac{x-a}{b-a}$。

• 数字特征：

  • 期望： $E(X)=\frac{a+b}{2}$ （区间的中点）

  • 方差： $D(X)=\frac{(b-a{)}^2}{12}$

---

2. 指数分布 (Exponential Distribution)

核心逻辑： “永远等待” & “无记忆性”。

它通常用来描述**“等待一个随机事件发生所需要的时间”**（如：等待下一次电话打入的时间、电子元件的寿命）。它是泊松过程在时间轴上的投影。

• 符号： $X\sim E(\lambda )$ （注意：教材中参数有时写为 $\theta$，关系是 $\lambda =1/\theta$）

• 概率密度函数 (PDF)：

  $f(x)=\{\begin{array}{ll}\lambda e^{-\lambda x},& x>0\\ 0,& x\le 0\end{array}$

  (其中 $\lambda >0$ 是失效率或发生率)

• 分布函数 (CDF)：

$F(x)=\{\begin{array}{ll}1-e^{-\lambda x},& x>0\\ 0,& x\le 0\end{array}$

• 关键性质：无记忆性

  $P(X>s+t|X>s)=P(X>t)$

  翻译： 假如你已经等了 $s$ 分钟，那么你需要“再等 $t$ 分钟”的概率，和你“一开始就等 $t$ 分钟”的概率是一样的。以前等的全白等了，元件像新的一样。

• 数字特征：

  • 期望： $E(X)=\frac{1}{\lambda }$

  • 方差： $D(X)=\frac{1}{{\lambda }^2}$

---

3. 正态分布 (Normal / Gaussian Distribution)

核心逻辑： “中间多，两头少” & “万物归宗”。

这是自然界最常见的分布（身高、体重、测量误差）。根据中心极限定理，大量独立随机变量之和近似服从正态分布。图像呈钟形曲线，对称优美。

• 符号： $X\sim N(\mu ,{\sigma }^2)$

• 概率密度函数 (PDF)： $f(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}},-\infty <x<+\infty$

  (决定位置的是 $\mu$，决定胖瘦的是 $\sigma$)

• 分布函数 (CDF)：

• $F(x)=\Phi \left(\frac{x-\mu }{\sigma }\right)$

• 标准正态分布：

  当 $\mu =0,\sigma =1$ 时，记为 $Z\sim N(0,1)$，其密度函数记为 $\phi (x)$，分布函数记为 $\Phi (x)$。任何正态分布都可以通过 $Z=\frac{X-\mu }{\sigma }$ 转化为标准正态分布查表计算。

• 数字特征：

  • 期望： $E(X)=\mu$

  • 方差： $D(X)={\sigma }^2$

---

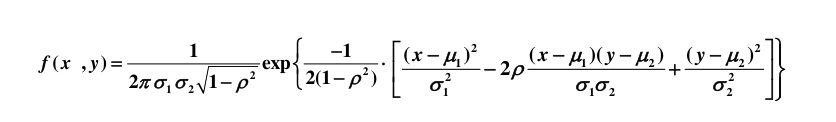
一图速览表

分布名称	记号	典型场景	期望 E(X)	方差 D(X)
均匀分布	$U(a,b)$	盲等公交、随机撒点	$\frac{a+b}{2}$	$\frac{(b-a{)}^2}{12}$
指数分布	$E(\lambda )$	排队等待、元件寿命	$\frac{1}{\lambda }$	$\frac{1}{{\lambda }^2}$
正态分布	$N(\mu ,{\sigma }^2)$	误差分析、统计规律	$\mu$	${\sigma }^2$